主成分分析PCA的分析及实现
1 原理分析
1.1 必要的数学概念
1.1.1 方差
方差 为离均差平方的算术平方值,用于描述一组数据的离散程度,计算公式为: \(s^2=\frac{{\mathrm{\Sigma}_{i=1}^n(X_i-\bar{X})}^2}{n-1}\)
1.1.2 协方差
方差和标准差中都只有X,是针对一维数据的,描述多维数据的离散程度可以使用协方差,二维数据的协方差 ,计算公式为: \(cov(X,Y)=\frac{\mathrm{\Sigma}_{i=1}^n(X_i-\bar{X})(Y_i-\bar{Y})}{n-1}\) 大于0,表示其中一维数据增大,另一维数据也会增大;
小于0 ,表示其中一维数据增大,另一维数据会减小;
=0,表示这二维数据相互独立。
容易知道: \(cov(X,X)=s^2\)
\[cov\left(X,Y\right)=cov\left(Y,X\right)\]1.1.3 协方差矩阵
对于多维数据,两两计算其协方差,协方差数量比较多,可以使用一个矩阵来保存这些结果,比如,二维数据的协方差矩阵为: \(C=\left(\begin{matrix}cov(X,X)&cov(X,Y)\\cov(Y,X)&cov(Y,Y)\\\end{matrix}\right)\) 三维数据的协方差矩阵为: \(C=\left(\begin{matrix}cov(X,X)&cov(X,Y)&cov(X,Z)\\cov(Y,X)&cov(Y,Y)&cov(Y,Z)\\cov(Z,X)&cov(Z,Y)&cov(Z,Z)\\\end{matrix}\right)\) 由前面的性质描述可以知道,协方差矩阵是对称矩阵。下图给出了二维数据X/Y相对独立、正相关、负相关时的三个例子:
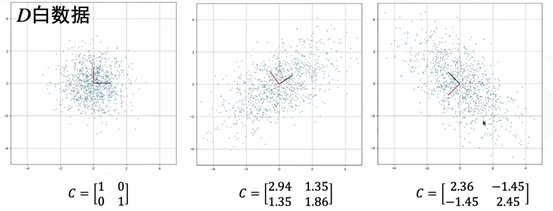
其中,白数据的协方差C0很明显为: \(C_0=\left(\begin{matrix}1&0\\0&1\\\end{matrix}\right)\)
1.1.4 特征值和特征向量
对于一个给定矩阵A,它的特征向量v经过一个线性变化之后,得到的新向量Av与原来的v保持在同一条直线上,但是其长度或者方向也许会改变,即: \(Av=\lambda v\) 其中lambda为标量,是特征向量的长度在该线性变化下缩放的比例,则称lambda为其特征值, v是A的特征向量。
特征值和特征向量很重要的一个特点是,不同特征值lambda对应的特征向量v是线性无关的,且对阵矩阵的特征向量两两正交。
1.2 PCA原理概述
PCA本质上是旋转坐标轴,找出使数据分散程度最大、保留信息最多的那个坐标轴。
以二维数据为例,二维数据D0经过中心化之后得到D,则D的协方差矩阵C还可以写为: \(C=\left(\begin{matrix}cov\left(X,X\right)&cov\left(X,Y\right)\\cov\left(Y,X\right)&cov\left(Y,Y\right)\\\end{matrix}\right)=\left(\begin{matrix}\frac{{\mathrm{\Sigma}_{i=1}^n\left(X_i-\bar{X}\right)}^2}{n-1}&\frac{\mathrm{\Sigma}_{i=1}^n\left(X_i-\bar{X}\right)\left(Y_i-\bar{Y}\right)}{n-1}\\\frac{\mathrm{\Sigma}_{i=1}^n\left(X_i-\bar{X}\right)\left(Y_i-\bar{Y}\right)}{n-1}&\frac{{\mathrm{\Sigma}_{i=1}^n\left(Y_i-\bar{Y}\right)}^2}{n-1}\\\end{matrix}\right) =\frac{1}{n-1}\left(\begin{matrix}X_1&X_2&X_3\\Y_1&Y_2&Y_3\\\end{matrix}\right)\left(\begin{matrix}X_1&Y_1\\X_2&Y_2\\X_3&Y_3\\\end{matrix}\right)=\frac{1}{n-1}D{D}^T\) D可由白数据D0经过拉伸S和旋转R变换得到,即: \(D=RSD_0\) D的协方差C可写为: \(C=\frac{1}{n-1}{DD}^T=\frac{1}{n-1}\ RSD_0{D_0}^TS^TR^T=\ RS\left({\frac{1}{n-1}D_0}{D_0}^T\right)S^TR^T=RSC_0S^TR^T =RS\left(\begin{matrix}1&0\\0&1\\\end{matrix}\right)S^TR^T=RSS^TR^T\) 其中C0是白数据D0的协方差。对于拉伸操作S和旋转操作R,有: \(S=S^T\)
\[R^T=R^{-1}\]则综上所述,令常数m为: \(m=SS^T=\left(\begin{matrix}a^2&0\\0&b^2\\\end{matrix}\right)\) 则C可写为: \(C=mRR^{-1}\) 即有: \(CR=mR\) 则m即为协方差矩阵C的特征值,R为其特征向量。同时m即为新坐标系下的协方差矩阵,其两个列向量分别表示在新坐标系下的方差。这样就相当于找到了将原数据转化为白数据的旋转坐标轴的办法。
将上述例子一般化,对于多维数据,可以求出其特征值矩阵,按照降维要求,取相应个数的列向量组成新的矩阵即为我们降维任务所需要的矩阵。流程总结如下图:
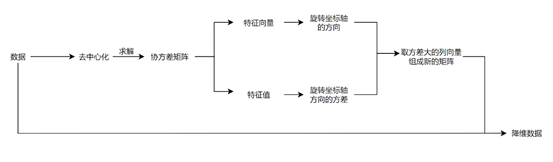
2 编程实现
import matplotlib.pyplot as plt
import numpy as np
plt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False # 用来正常显示负号
# 数据
x = np.array([9, 16, 25, 14, 10, 18, 0, 16, 5, 19, 16, 20])
y = np.array([39, 57, 93, 61, 50, 75, 32, 85, 42, 70, 66, 80])
z = np.array([7, 58, 73, 1, 0, 55, 72, 87, 4, 10, 86, 30])
D0 = np.zeros([12, 3]) # 创建一个12行x3列的零矩阵
D0[:, 0] = x
D0[:, 1] = y
D0[:, 2] = z
print("原数据:\n", D0)
print("原数据的维数: \n", D0.shape)
# 中心化
D0_Av=np.mean(D0, axis=0)
print("均值:",D0_Av)
D = D0 - D0_Av
print("中心化之后:\n", D)
print("中心化数据的维数: \n", D.shape)
# 绘制中心化对比图
ax = plt.subplot(111, projection='3d')
for i in range(0, 12):
ax.scatter(D[i][0], D[i][1], D[i][2], c='b')
for i in range(0, 12):
ax.scatter(D0[i][0], D0[i][1], D0[i][2], c='r')
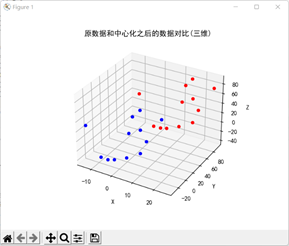
plt.title("原数据和中心化之后的数据对比(三维)")
ax.set_zlabel('Z')
ax.set_ylabel('Y')
ax.set_xlabel('X')
plt.show()
# 绘制中心化对比图(投在二维上)
plt.scatter(D0[:, 0], D0[:, 1], label='原数据(XY方向投影)')
plt.scatter(D[:, 0], D[:, 1], label='中心化之后(XY方向投影)')
plt.xlabel('X')
plt.ylabel('Y')
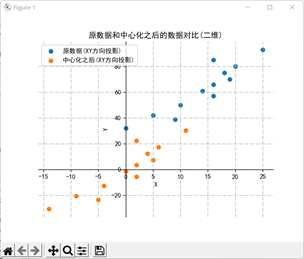
plt.title("原数据和中心化之后的数据对比(二维)")
plt.legend()
plt.grid(True, linestyle='-.')
ax = plt.gca() # 获取当前坐标的位置
ax.spines['right'].set_color('None') # 去掉坐标图的上和右的黑边
ax.spines['top'].set_color('None')
ax.xaxis.set_ticks_position('bottom') # 设置bottom为x轴
ax.yaxis.set_ticks_position('left') # 设置left为y轴
ax.spines['bottom'].set_position(('data', 0)) # 这个位置的括号要注意
ax.spines['left'].set_position(('data', 0))
plt.show()
# 计算协方差矩阵
Cov1 = np.mat(D.T) * np.mat(D) / (len(x) - 1)
print("协方差矩阵:\n", Cov1)
print("协方差矩阵的维数: \n", Cov1.shape)
# 计算特征值、特征向量
Cov2 = np.cov(D, rowvar=False)
eigVals, eigVects = np.linalg.eig(np.mat(Cov2))
print("特征值: \n", eigVals)
print("特征向量的矩阵: \n", eigVects)
print("特征向量的矩阵的维数: \n", eigVects.shape)
# 统计哪些是主成分
tot = sum(eigVals)
eigVals_exp = [(i / tot) for i in sorted(eigVals, reverse=False)] # 特征值的贡献率
cum_eigVals_exp = np.cumsum(eigVals_exp) # 累积特征值的贡献率
# 绘制特征值的贡献率与累计贡献率,用来判断主成分
plt.bar(range(0, 3), eigVals_exp, alpha=0.25, label='贡献率')
plt.plot(range(0, 3), cum_eigVals_exp, marker='o', label='累计贡献率')
plt.ylabel('贡献率')
plt.xlabel('index')
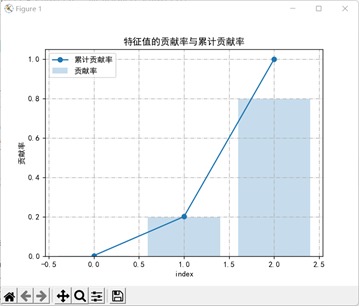
plt.title("特征值的贡献率与累计贡献率")
plt.legend()
plt.grid(True, linestyle='-.')
plt.show()
# 截取出主成分
eigVects_main = eigVects[:, 1:3] # 截取所有行,前1~3-1共2列,截取的后两维数据作为主成分
print("截取的特征向量的矩阵: \n", eigVects_main)
print("截取的特征向量的矩阵的维数: \n", eigVects_main.shape)
#使用截取的矩阵来降维中心化的数据
D_main = np.matmul(D, eigVects_main)
print("降维的中心化的矩阵: \n", D_main)
print("降维的中心化的矩阵的维数: \n", D_main.shape)
#中心化,恢复最原始的数据
D0_main = D_main + D0_Av[1:3]
print("降维的原矩阵: \n", D0_main)
print("降维的原矩阵的维数: \n", D0_main.shape)
# 绘制降维对比图
ax = plt.subplot(111, projection='3d')
for i in range(0, 12):
ax.scatter(D0[i][0], D0[i][1], D0[i][2], c='b')
for i in range(0, 12):
ax.scatter(0, D0_main[i][0], D0[i][1], c='r')
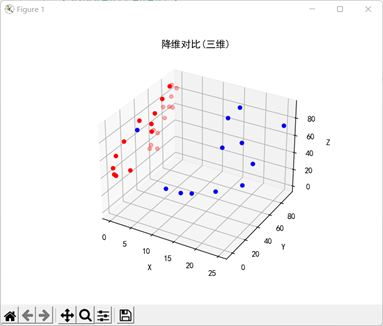
plt.title("降维对比(三维)")
ax.set_zlabel('Z')
ax.set_ylabel('Y')
ax.set_xlabel('X')
plt.show()
原数据:
[[ 9. 39. 7.]
[16. 57. 58.]
[25. 93. 73.]
[14. 61. 1.]
[10. 50. 0.]
[18. 75. 55.]
[ 0. 32. 72.]
[16. 85. 87.]
[ 5. 42. 4.]
[19. 70. 10.]
[16. 66. 86.]
[20. 80. 30.]]
原数据的维数:
(12, 3)
均值: [14. 62.5 40.25]
中心化之后:
[[ -5. -23.5 -33.25]
[ 2. -5.5 17.75]
[ 11. 30.5 32.75]
[ 0. -1.5 -39.25]
[ -4. -12.5 -40.25]
[ 4. 12.5 14.75]
[-14. -30.5 31.75]
[ 2. 22.5 46.75]
[ -9. -20.5 -36.25]
[ 5. 7.5 -30.25]
[ 2. 3.5 45.75]
[ 6. 17.5 -10.25]]
中心化数据的维数:
(12, 3)
协方差矩阵:
[[ 48. 122.54545455 57.81818182]
[ 122.54545455 369. 273.59090909]
[ 57.81818182 273.59090909 1226.56818182]]
协方差矩阵的维数:
(3, 3)
特征值:
[ 5.51753909 325.20159797 1312.84904476]
特征向量的矩阵:
[[-0.93960903 0.33471716 0.07140937]
[ 0.34076353 0.89551555 0.28623787]
[-0.03186053 -0.29328539 0.9554939 ]]
特征向量的矩阵的维数:
(3, 3)
截取的特征向量的矩阵:
[[ 0.33471716 0.07140937]
[ 0.89551555 0.28623787]
[-0.29328539 0.9554939 ]]
截取的特征向量的矩阵的维数:
(3, 2)
降维的中心化的矩阵:
[[-12.96646198 -38.85380876]
[ -9.4617169 15.52852713]
[ 21.3900165 40.80818307]
[ 10.16817828 -37.93249223]
[ -0.72807603 -42.32224013]
[ 8.2068535 17.95714577]
[-41.31107572 20.60694514]
[ 7.10744216 51.25251039]
[-10.7389278 -41.14721431]
[ 17.26183552 -26.39985953]
[ -9.6140679 44.85849703]
[ 20.68600036 -4.35619357]]
降维的中心化的矩阵的维数:
(12, 2)
降维的原矩阵:
[[49.53353802 1.39619124]
[53.0382831 55.77852713]
[83.8900165 81.05818307]
[72.66817828 2.31750777]
[61.77192397 -2.07224013]
[70.7068535 58.20714577]
[21.18892428 60.85694514]
[69.60744216 91.50251039]
[51.7610722 -0.89721431]
[79.76183552 13.85014047]
[52.8859321 85.10849703]
[83.18600036 35.89380643]]
降维的原矩阵的维数:
(12, 2)